ABC197 D問題 Opposite 座標問題を解く - 競技プログラミング悪戦苦闘日記

ABC197 D問題 Oppositeを解いて振り返ります。

2次元座標に正N角形があって、各頂点 $p_0, p_1, p_{N-1}$ が与えられています。
Nは偶数。 $p_0$ と $p_{\frac N 2}$ の座標が与えられた時に $p_1$ の座標を求める問題です。

高校数学を駆使して解ける問題です。
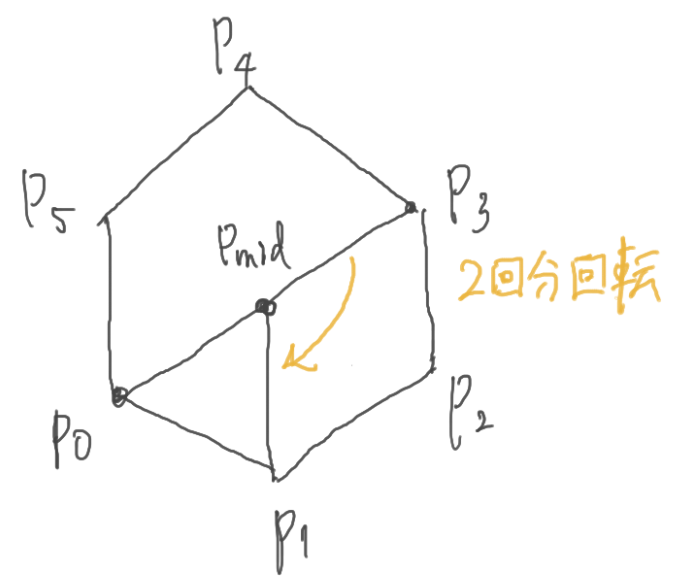
サンプルのように正六角形の場合、 $p_0$ と $p_3$ の座標が与えられます。
$p_0$ と $p_3$ の中点が正六角形の中心になるので、そこを中心に $2 \times 360 / 6$ 度時計回りに回転したところが $p_1$ の座標になります。

f:id:hrksb5029:20210328024022p:plain

座標 $(x, y)$ を $\theta$ 反時計回りに回転させるときは、
$\left( \begin{array}{rr} cos\theta & -sin\theta \\ sin\theta & cos\theta \end{array} \right)\left(\begin{array}{r}x \\ y\end{array}\right)$
となります。
$p_3$ を回転させる前に、座標が原点に来るように中点の分だけ平行移動させて、回転した後に中点の分だけ平行移動して戻します。

回転する度数としては、 $360 / N$ 度を2回分時計回りに回転します。時計回りなので $\theta$ に-1をかけます。
$\theta = - \frac {2\pi} {N} \times (\frac N 2 - 1) = \frac {2\pi} {N} - \pi$

座標を求める式は以下のようになります。

f:id:hrksb5029:20210328024048p:plain

なので、x座標を求める式は以下のようになります。
$cos\left( \frac {2\pi} {N} - \pi \right) \times \left(x_{\frac N 2} - x_{mid}\right) - sin\left( \frac {2\pi} {N} - \pi \right) \times \left( y_{\frac N 2} - y_{mid} \right) + x_{mid}$

y座標を求める式は以下のようになります。
$sin\left( \frac {2\pi} {N} - \pi \right) \times \left(x_{\frac N 2} - x_{mid}\right) + cos\left( \frac {2\pi} {N} - \pi \right) \times \left( y_{\frac N 2} - y_{mid} \right) + y_{mid}$

from math import pi, cos, sin
N = int(input())
x0, y0 = map(int, input().split())
x_N_2, y_N_2 = map(int, input().split())
x_mid = (x0 + x_N_2) / 2
y_mid = (y0 + y_N_2) / 2

deg = (2*pi/N) - pi

cos_deg = cos(deg)
sin_deg = sin(deg)

ans_x = cos_deg * (x_N_2 - x_mid) - sin_deg * (y_N_2 - y_mid) + x_mid
ans_y = sin_deg * (x_N_2 - x_mid) + cos_deg * (y_N_2 - y_mid) + y_mid

print(ans_x, ans_y)